Hexagonal Grids! A Puzzle Bobble Tutorial

So I have finally gotten through my gba game. Its a Puzzle Bobble clone with a spooky/haunted house aesthetic; Made on Notepad++, using C as well as ARM assembly. It follows a standard C structured code architecture with things such as manual interface classes (Given C doesn’t actually support interfaces)
Check it out!
This project started as a university hand-in; I really wanted to get an entire game finished for my deadline but unfortunately i missed a lot of major Puzzle Bobble features before i had to wrap it up (Even then i handed it in a month later , getting a capped mark; But hey, I passed) A major one is the Hex Grid, which i will try and simplify on this entry!

What is a Hex Grid?

Well…something like what this crappy drawing is trying to illustrate.

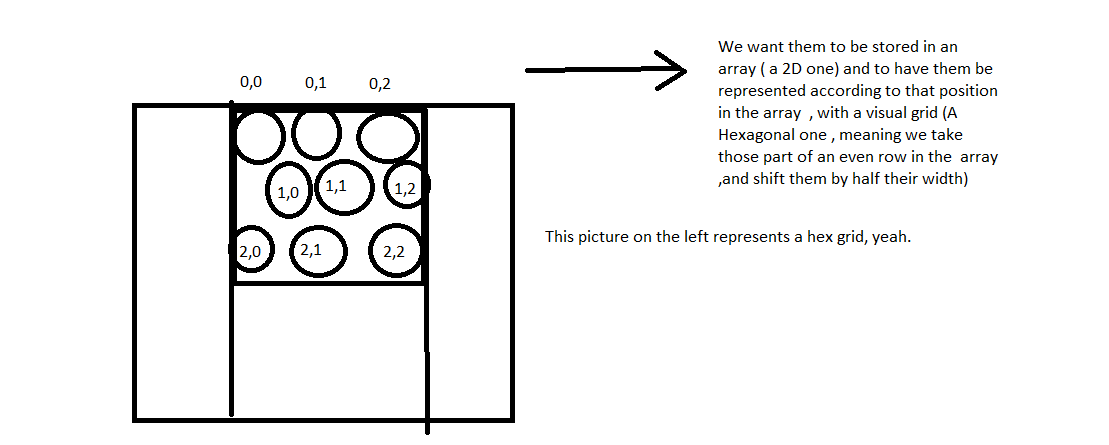
A Hexagonal Grid, or Isometric grid , is a cell based coordinate system where every other row is offset by cellSize/2. It’s quite similar to a quadratic grid (One without the offset), except every cell gets two extra direct neighbours. Feel free to skip this one , which we will touch upon on another entry, when we try to analyze ball chains.

And for my game:

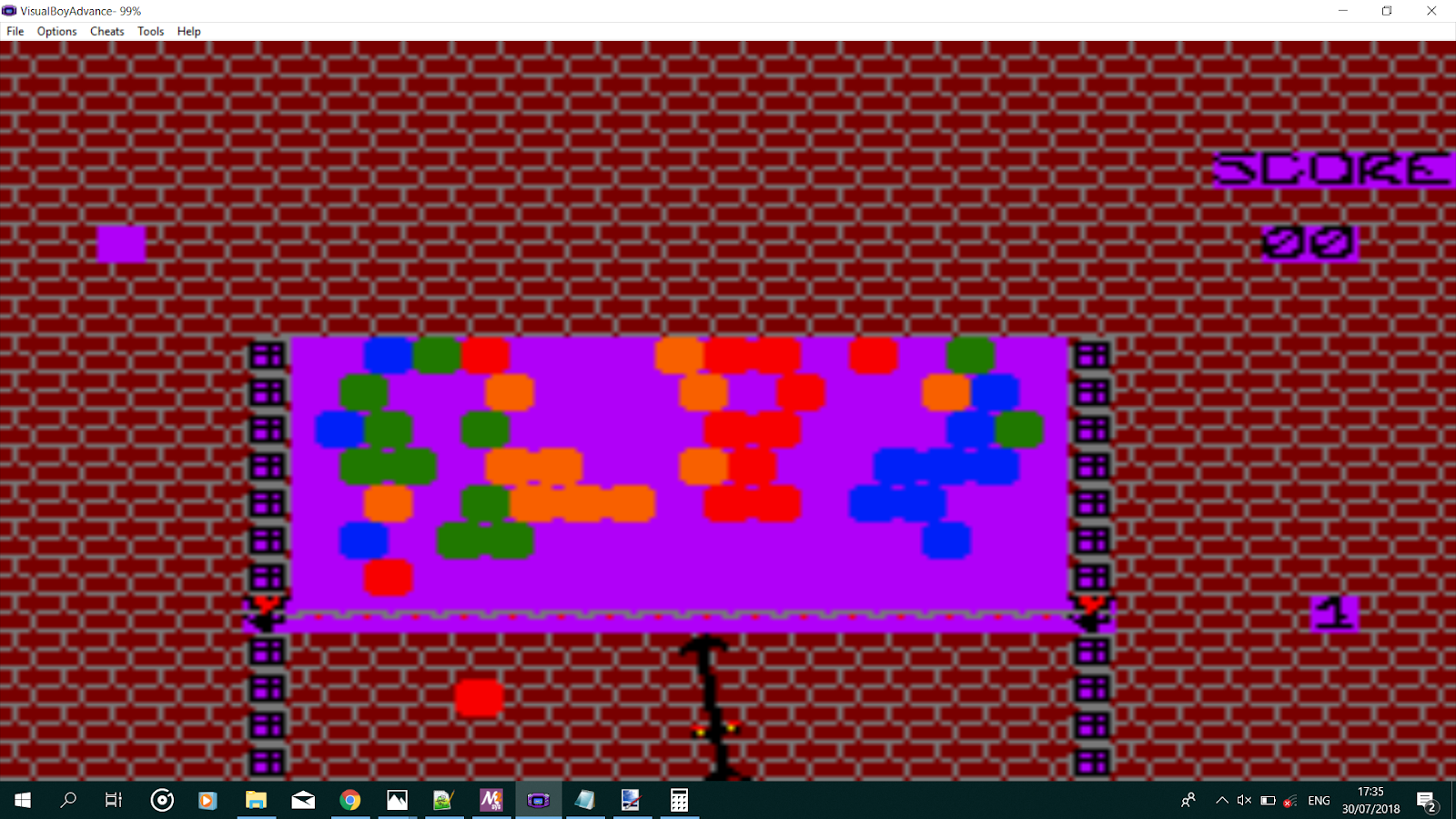
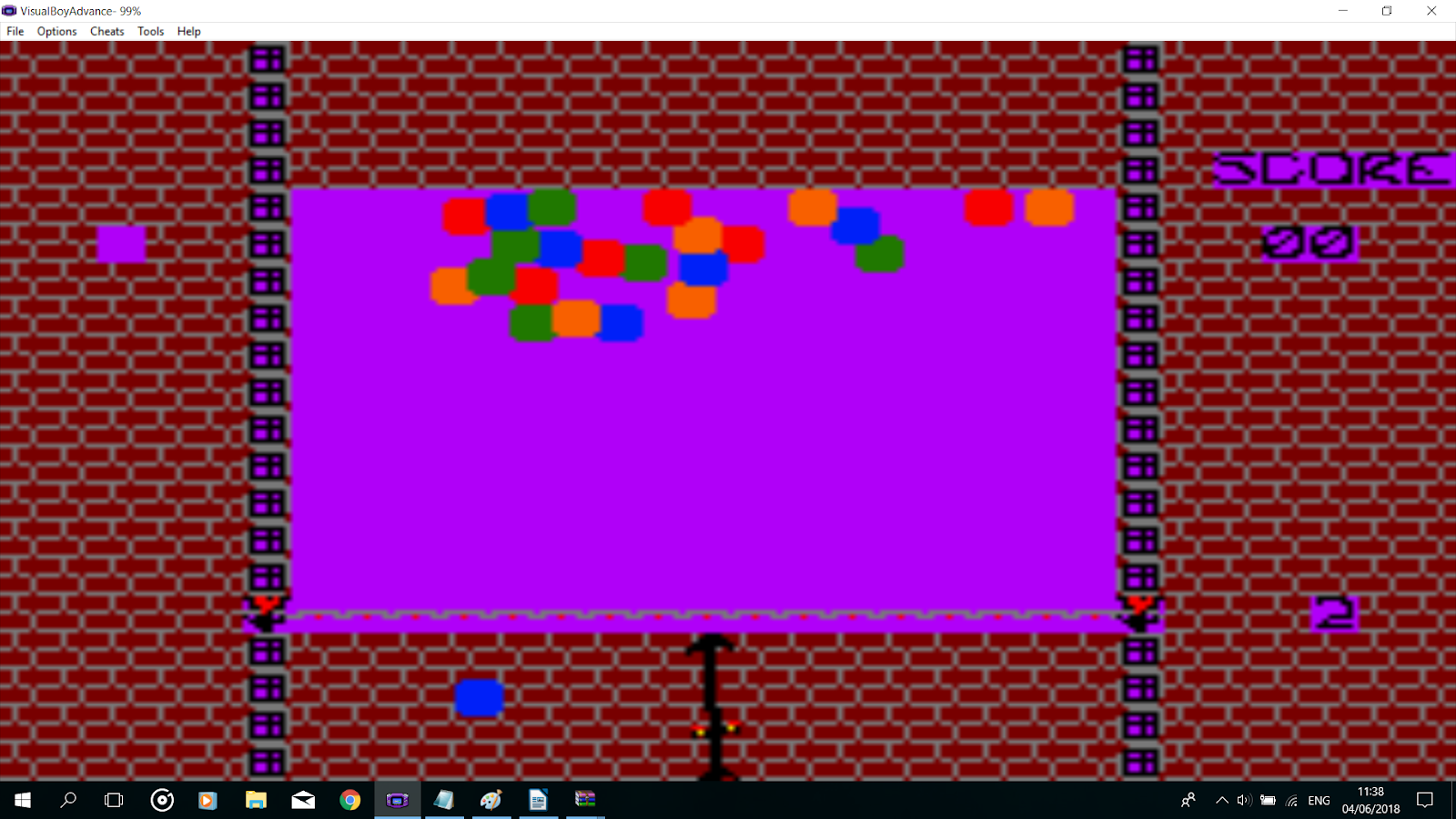
See the difference? The first one looks much more organized , doesn’t it? Not only that but it makes a lot of the important calculations (Identifying chains of X balls, Finding floating balls,…) used in Puzzle bobble, which I might look into on later entries, accurate and actually doable!

Implementation

Alright. So for my approach, I had a 2d array as a way of storing my grid. This array was filled with instances of a custom struct, which included a presetPos Vector2 variable (another struct with two ints, an x and y coordinate), for odd rows, I would apply the offset, just like on the first two pictures. This is the way i felt most comfortable for storing my data, however i was working in C /ARM code with its limitations creating a gba rom (even more limitations), which is why I avoided pointers, since I wasn’t fond of malloc() and free() pointer calls. The API you use will determine your approach.

Now, in order to set, or update this grid, I would run through my 2d array using a nested for loop, executing code akin to this on all the static balls (Those already snapped to the grid)

//Set position of the grid
   theStaticBall->presetPos.x = X_MIN +  col*BALL_SIZE
   //Screen coordinates (y is down)
   theStaticBall->presetPos.y = CEILING_OFFSET + row*BALL_SIZE
   theStaticBall->maxExtent.x = theStaticBall->presetPos.x + BALL_SIZE*N;
   theStaticBall->maxExtent.y = theStaticBall->presetPos.y + BALL_SIZE*N;
   if (row % 2){
    //If row is odd (hexGrid) we offset by halfWidth
    theStaticBall->presetPos.x += BALL_SIZE/2;
    theStaticBall->maxExtent.x += BALL_SIZE/2;
   }

Then i would analyze if we dropped below the threshold (The little rope in puzzle bobble), and finally redraw. One recommendation for 2D arrays is that you set it up in a [column][row] fashion, so that it makes the for loop intuitive as it mimmicks [x][y] coords.

Grid Snapping

Okay, so we know how to refresh our grid (ceiling drop), but how do we actually snap our ball to this 2d array? We need to turn our game coordinates (In my case screen coordinates) into grid positions! Meaning 2d array slots.
At this point you’d have figured that one of the disadvantages of my 2d array is that no matter how many balls are on screen, you will always be occupying the same (considerable) amount of data, just that the empty array slots will be filled with zeroes. In my case it was a [16][15] array. Pointers would be a good workaround, however this is much simpler to understand.

This is basically the opposite operation than before.

///SNAP TO GRID
 //Convert screen coordinate to  gridPosition
 //X: Dist from row beginning
 float offSetX = movingBall.position.x - X_MIN;//0-128 in my case
 //Y: Dist from roof
 float offSetY = myGs->movingBall.position.y - myGs->yOffset;
 int gridX;
 int gridY = round(offSetY/BALL_SIZE);
 if ((gridY % 2)){
  //If its odd row
  offSetX -= BALL_SIZE/2;
 }
 gridX = round(offSetX/BALL_SIZE);

We find its distance from what’s considered the left/top edge , and we divide it by BALL_SIZE (8x8 for mine) However, for odd rows (or even) we need to get rid of that offset, before we divide it, in order to find the right grid position. Once there, I just had to fill the array cell with the movingBall’s values, and clear it.

I think that’s it for the basics! This is my first post, so any feedback/recommendations are helpful. Congrats for getting through!

If you’re interested in learning about the rest of the features you can always check out my github repository. The functions are fairly similar, except I make use of Fixed Point Arithmetic in order to use floats in gba (needed for angles , etc). That is a subject that I probably won’t cover , but is pretty well explained here.

Alright, enough ball quotes for today.